Summary: How These Concepts Help Solve Word Problems
Parabola
- Definition:
- A parabola is the curved graph of a quadratic function.
- Every point on the parabola is equally distant from a fixed point (called the focus) and a fixed line (called the directrix).
- In Math:
- Appears in algebra as the graph of equations like
- y = ax^2 + bx + c
- conic sections in geometry
- Word Problems:
- Modeling objects in flight (projectile motion)
- Designing satellite dishes, flashlights, and reflectors
Vertex
- Definition:
- The vertex is the turning point of a parabola — the highest or lowest point depending on the direction it opens.
- From vertex form y=a(x−h)2+k, the vertex is (h,k).
- In Math:
- Used to find maximum or minimum values of a quadratic.
- Word Problems:
- Maximum height of a thrown ball
- Minimum cost in a budgeting problem
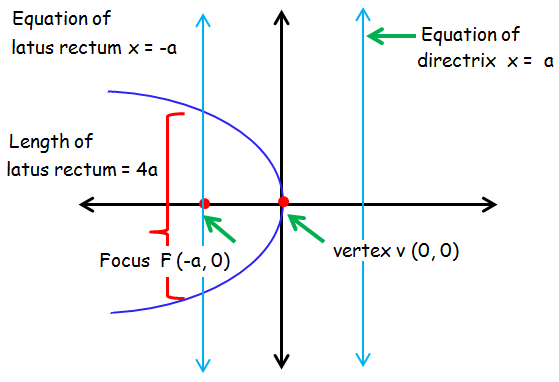
Focus
- Definition:
- A fixed point inside the parabola that, along with the directrix, defines the shape of the parabola.
- In Math:
- The parabola contains all points equidistant from the focus and directrix.
- Word Problems:
- Signal design (e.g., satellite or radar dishes)
- Sound projection in theater architecture
Directrix
- Definition:
- A fixed line outside the parabola. Every point on the parabola is the same distance from the focus and the directrix.
- In Math:
- Used in the geometric definition of parabolas.
- Word Problems:
- Helps determine symmetry in technical and architectural designs
Axis of Symmetry
- Definition:
- A vertical or horizontal line that divides the parabola into two mirror-image halves.
- If the parabola is y=a(x−h)2+k, the axis is x=h.
- In Math:
- Used to analyze symmetry and find the vertex quickly.
- Word Problems:
- Reflective symmetry in design problems
- Finding balance points in optimization tasks
Focal Length
- Definition:
- The distance from the vertex to the focus. Determines how “wide” or “narrow” the parabola is.
- In Math:
- Focal Length=
- Focal Length=
- Word Problems:
- Used in lens and mirror designs (concentrating or dispersing light)
- Controls beam width in flashlights or projectors
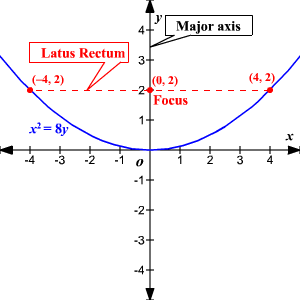
Latus Rectum
- Definition:
- A line segment that passes through the focus and is perpendicular to the axis of symmetry.
- Its endpoints lie on the parabola, and its length (called the focal width) is 4f, where f is the focal length.
- In Math:
- Measures the “thickness” of the parabola near the focus.
- Word Problems:
- Precision lens crafting (how much light the lens captures)
- Radio telescope dish width near focal point
Intercepts
- Definition:
- X-intercepts: Where the parabola crosses the x-axis (set y=0)
- Y-intercept: Where the parabola crosses the y-axis (set x=0)
- In Math:
- Used to solve quadratic equations and sketch graphs.
- Word Problems:
- X-intercepts can represent time when an object hits the ground
- Y-intercepts may show starting height or value (initial conditions)
| Concept | Solves Problems Like… |
| Parabola | Modeling motion, designing reflectors or projectiles |
| Vertex | Finding maximum height, minimum cost/value |
| Focus | Signal or sound targeting, architectural focus design |
| Directrix | Helps define symmetry and structure layout |
| Axis of Symmetry | Balanced design, simplifies graphing |
| Focal Length | Determines curve width, light or signal direction |
| Latus Rectum | Measures light/sound capture area near the focus |
| Intercepts | Starting point or landing time, solving equations |

Quiz
1. MULTIPLE CHOICE QUESTION
1 pt

What are the arrows pointing to?
a. x-intercept(s)
b. y-intercept(s)
c. vertex
d. line of symmetry
2. MULTIPLE CHOICE QUESTION
1 pt

What is the arrow pointing to?
a. x-intercept(s)
b. y-intercept(s)
c. vertex
d. line of symmetry
3. MULTIPLE CHOICE QUESTION
1 pt

What is the arrow pointing to?
a. x-intercept(s)
b. y-intercept(s)
c. vertex
d. line of symmetry
4. MULTIPLE CHOICE QUESTION
1 pt
Which one shows the correct line of symmetry?
a. 1st chart
b. 2nd chart
c. 3rd chart
d. 4th chart




5. MULTIPLE CHOICE QUESTION
1 pt

Where is the vertex on the parabola?
a. (0,12)
b. (1,0)
c. (2,-4)
d. (3,0)
6. MULTIPLE CHOICE QUESTION
1 pt

Where is the minimum of the parabola?
a. (0,12)
b. (1,0)
c. (2,-4)
d. (3,0)
7. MULTIPLE CHOICE QUESTION
1 pt
The graph of a quadratic function is called a
a. Parabola
b. Vertex
c. Axis of Symmetry
d. Vertex Form
8. MULTIPLE CHOICE QUESTION
1 pt

What is the green-dashed line called?
a. roots or x-intercepts
b. parabola
c. axis of symmetry
d. line of dashes
9. MULTIPLE CHOICE QUESTION
1 pt
The axis of symmetry line passes through which point?
a. y-intercept
b. any random point
c. vertex
d. symmetrical point for the vertex
10. MULTIPLE CHOICE QUESTION
1 pt

What is this point called?
a. axis of symmetry
b. vertex
c. quadratic
d. parabola
11. MULTIPLE CHOICE QUESTION
Is the leading coefficient of the equation of this parabola a positive or a negative value?
a. positive
b. negative
c. impossible to determine
12. MULTIPLE CHOICE QUESTION
What are the coordinates of the y-intercept of a parabola, represented by the following equation:
y = 2x² – 3x + 5
a. (0,2)
b. (0,-3)
c. (0,5)
13. MULTIPLE CHOICE QUESTION
Complete the square to convert this standard form equation into a vertex form equation:
y = 2x² + 8x – 14
State the coordinates of the vertex
a. (2, 22)
b. (-4, -14)
c. (-2, -22)
14. MULTIPLE CHOICE QUESTION
State the coordinated of the vertex of the parabola represented by the following equation:
y = -2(x -3)² + 24
a. (-2, -3)
b. (-3, -24)
c. (3, 24)
14. MULTIPLE CHOICE QUESTION
What is a real life example of a quadratic function?
a. a competitive swimmer swimming
b. a basketball flying into the net
c. a train moving at a certain speed

